この記事はPython その2 Advent Calendar 2015 の17日目の記事です。
1 はじめに
雇用統計のモデルで有名なにほんばっしー(現在活動停止中?)が公開していた予想方法を元に、雇用統計の数値を予想するモデルを作成してみます。
2 モデル作成
2.1 使用する指標
ザイのリンクからにほんばっしーが使っていた指標は以下となっています。
- 新規失業保険申請件数
- ニューヨーク連銀製造業景気指数の「雇用」
- フィラデルフィア連銀製造業景況指数の「雇用」
- ミシガン大学消費者信頼感指数
- カンザスシティ連銀製造業景況指数の「雇用」
- ダラス連銀製造業活動指数の「雇用」
- リッチモンド連銀製造業景況指数の「雇用」
- 消費者信頼感指数の「雇用不十分」
- 消費者信頼感指数の「雇用困難」
- 米ドル/円変化率(1カ月前)
- ISM製造業景況指数の「雇用」
- S&P500指数変化率(1カ月前)
- ADP雇用統計
- チャレンジャー人員削減予定数
このうち、無料では入手が困難だったカンファレンスボード関連の消費者信頼感指数の「雇用不十分」、「雇用困難」を除いた指標を使うことにします。まとめたデータを公開したいのですが、二次公開には色々と成約が付きまとうので今回は残念ながら公開できません。代わりにリンクをまとめておきます。
ここでは、"Summery Of Indexes.xlsx"というエクセルファイルにデータを保存しました。
2.2 単純に重回帰分析をしてみる
"Summery Of Indexes.xlsx"のファイルのTrainというシートのデータを取得します。
import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
data_table = pd.read_excel("Summary Of Indexes.xlsx", sheetname="Train")
data_table.head()
statsmodels.api.OLSを使えば、簡単に重回帰分析をした結果を取得できます。
# Read Data
y = data_table[u"新規失業保険申請者数"]
x = data_table[[u"NY連銀雇用", u"フィラデルフィア連銀雇用", u"ミシガン大指数", u"カンザスシティ連銀雇用",
u"ダラス連銀雇用", u"リッチモンド連銀雇用", u"ISM製造雇用", u"S&P500 変化率1ヶ月遅行", u"ADP雇用統計",
u"チャレンジャー人員削減数"]]model = sm.OLS(y, x)
model = sm.OLS(y, x)
results = model.fit()
results.summary()
結果をプロットしてみます。
import matplotlib.pyplot as plt plt.plot(results.predict(), "r") plt.plot(y, "b")
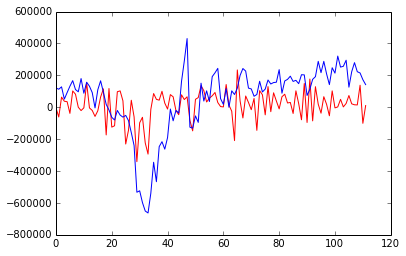
青が実際の値で、赤が予測値です。
パッと見でなんとなくいけてなさそうですが、訓練データとしてしか使っていないのでこれだけでは実際の予測能力の評価ができません。
2.3 交差検証(Cross Validation)する
訓練データとテストデータに分けて評価してみます。あまりデータ数がないので、Leave One Out Cross Validation を用いることにします。
Leave One Out はscikit-learnに便利な module LeaveOneOut が提供されているのでそれを用いることにします。
from sklearn.cross_validation import LeaveOneOut
LeaveOneOut検証を行った後の結果を返す method を作成します。targetに予想したい結果を入れて、予想に使う要素をinputsに入れます。
def make_prediction(target, inputs):
loo = LeaveOneOut(len(data_table))
predict_results = []
for train, test in loo:
train_table = data_table.iloc[train]
test_table = data_table.iloc[test]
y_train = train_table[target]
x_train = train_table[inputs]
y_test = test_table[target]
x_test = test_table[inputs]
model = sm.OLS(y_train, x_train)
result = model.fit()
calc_prediction = (result.params * x_test)
prediction = calc_prediction.sum().sum()
predict_results.append(prediction)
return predict_results
target = u"雇用統計結果"
inputs = [u"新規失業保険申請者数", u"NY連銀雇用", u"フィラデルフィア連銀雇用", u"ミシガン大指数", u"カンザスシティ連銀雇用",
u"ダラス連銀雇用", u"リッチモンド連銀雇用", u"ISM製造雇用", u"S&P500 変化率1ヶ月遅行", u"ADP雇用統計",
u"チャレンジャー人員削減数"]
predicts = make_prediction(target, inputs)
actuals = data_table[u"雇用統計結果"]
forecasts = data_table[u"雇用統計予想値"]
import matplotlib.pyplot as plt
plt.plot(predicts, "r")
plt.plot(actuals, "b")
plt.plot(forecasts, "g")
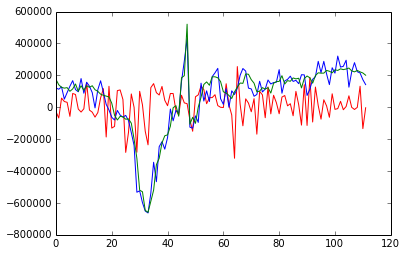
predicts にはLeaveOneOut検証によって得られた結果だけを格納されています。全然いけてないですね・・。
2.4 アナリスト予想に対する方向性の精度を検証
一応、アナリストの予想値と結果の方向性をどのぐらい予想出来ているかを計算してみます。
# calc predictive accuracy
def accurates_and_faults(predicts, actuals, forecasts):
accurates = 0
faults = 0
for p, a, f in zip(predicts, actuals, forecasts):
if (f p):
faults += 1
elif(f > a):
if(f > p):
accurates += 1
elif(f
accurates, faults = accurates_and_faults(predicts, actuals, forecasts) print "accurates: %d, faults: %d accurate ratio: %f"%(accurates, faults, accurates * 1.0 / (accurates + faults)) # accurates: 59, faults: 52 accurate ratio: 0.531532
予想値と結果のずれの方向性を59回的中させ、52回失敗し、的中率は53%となりました。
2.5 アナリスト予測に対する精度を検証
これもまた一応ですが、結果とのずれ具合を検証してみます。
def calc_diff(inputs, targets):
diff_sum = 0
for i, t in zip(inputs, targets):
diff_sum += abs(t - i)
return diff_sum
sum_diff_predict = calc_diff(predicts, actuals)
sum_diff_forecast = calc_diff(forecasts, actuals)
print "difference against forecasts: %f"%(sum_diff_predict*1.0 / sum_diff_forecast)
# difference against forecasts: 3.394691
アナリストの予想に対し、今回のモデルの予想精度は約3.4倍劣る結果となりました。
3 作りこんでいけば・・
Cross Validation で使うべき要素を選別、精度を高めていけば、それなりに予測能力を持つモデルを作成できるようになります。下が実際に作成しているモデルから得られた出力例です。独自に追加した要素などを使えば、このぐらいの精度までは出せました。今のところ、2回連続的中しています。
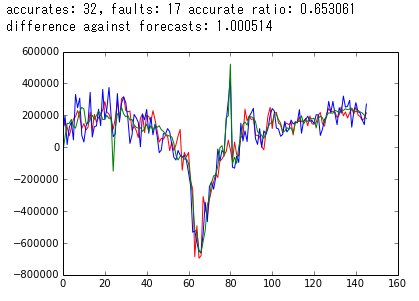
3.1 実際に予想した結果
11月
https://twitter.com/fx_kirin/status/662107829646417920
https://twitter.com/okasanman/status/662622972822224896
12月
https://twitter.com/fx_kirin/status/672617841145741312
https://twitter.com/okasanman/status/672769835625922560
ipython データ
あとがき
なんか書いてみるとあんまりPython関係ないのかなと思ったり思わなかったり。こういう情報って使えるもの出すと色々怖いので、丁度いい案配だったんじゃないかなぁと思います。






コメント