洋書を読んでいると、いつも読んだ気になってちゃんと理解出来てるか自信がないことが多いので、チャプターごとに要点をまとめて、理解を深めていきたい。
読んでいる本はこちら。金融素人の私にとっては、デリバティブについて深く学ぶいい機会になってます。少しでも参考になったら、ここでは詳細には触れませんのでぜひ購入を検討してみてください。この本を片手に参考程度に見てもらえればと思っています。
[rps-include post=”2280″]
A Quick Tour
Market-Based Valuation
Market-Based Valuation という言葉だが、適切な日本語訳というのがまだ定まってないのか見つからない。英語 Wiki にはページがある。
各チャプターについてや、この本の構成についての概要を説明している。
What is Market-Based Valuation?
Options and their values
オプションは売りと買いの取引ができ、売り手を Option Writers, 買い手を Option Holders と呼ぶ。
ヨーロピアンオプションを例に考える。
権利執行価格(ストライク価格)の8,000で満期時の価格が8,200だとすると、 Optiojn Holder は200の価値を受け取ることになる。すなわち、Option Writer は 200支払うことになる。権利行使価格が7,800だった場合には、Option Writerは何も支払う必要はない。(損失はOption Holderが払うことになるから)
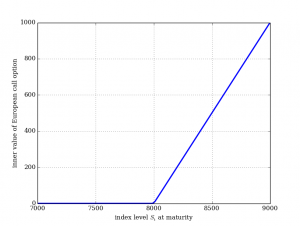
このオプションの内的価値を数式にしてみると下式になる。
[latex]h_T(S, K) = \max[S_T – K, 0][/latex]
[latex]T[/latex]:権利執行日 [latex]S_T[/latex]:権利行使価格 [latex]K[/latex]:満期時の価格
Pythonでコードを書いて、matplotlibでグラフ描写するとこんな形になる。
| in-the-money(ITM) | 利益が出ている状態 call => S > K, put => S < K |
|---|---|
| at-the-money(ATM) | 権利行使価格と満期時の価格が同じ状態 S = K |
| out-of-the-money(OTM) | 利益が出ていない状態 call => S > K, put => S > K< K |
先ほどのグラフは、満期時のオプションの価値を表したものだけのものである。満期以前のオプションの現在の価値をモデル化できれば、金融商品として扱うことができるようになる。
| initial index level | 現在のインデックスの価格 |
|---|---|
| initial index level | インデックスのボラティリティ |
| initial index level | 満期までの時間 |
| initial index level | 金利 |
今回のようなバニラオプションでは、ブラック・ショールズモデルが使われる。
[latex]C^*_0 = C^BSM(S_0, K, T, r, \sigma)[/latex]
[latex]C^*_0[/latex] 現在のヨーロピアンオプションの価格 [latex]C^BSM[/latex] ブラック・ショールズ方程式
| [latex]S_0[/latex] | 現在の価格 |
|---|---|
| [latex]K[/latex] | 権利行使価格 |
| [latex]T[/latex] | 満期までの時間 |
| [latex]r[/latex] | risk-less short rate 固定値 |
| [latex]\sigma[/latex] | インデックスのボラティリティ |
このブラック・ショールズ方程式を導入した先ほどのグラフを同様にPythonで書くとこのようになる。
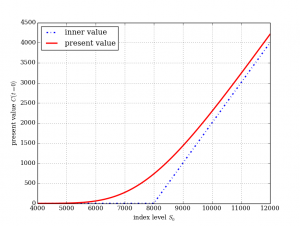
赤の価格がオプションの現在の価格となるわけである。
2.2 Vanilla vs. Exotic Instruments
オプションにはバニラオプションとエグゾティックオプションの2種類がある。
バニラオプションは2.1で紹介したような古典的なオプション。エグゾティックオプションはバリアオプションやバイナリーオプションのような売りと買いだけでは単純に区別できないオプション。
エグゾティックオプションは単純じゃないからしっかりモデルを立てて、フェアな価格を提供しなければならない。
どのようなモデルであろうと、エグゾティックオプションの価値付けとヘッジをするために使うときには、質的特徴と量的特徴の両方を注意深く考慮しなければならない。
| 質的特徴 | ある推測を立てたとしても、それが適切でない可能性があること |
|---|---|
| 量的特徴 | 価格変動に影響を及ぼしうる対象は一般的に無限に多いこと |
これらの要素については、後のチャプターで説明していく。
Risks Affecting Equity Derivatives
デリバティブの価格に影響を与えるマーケット・リスクについての章。
Market Risks
| price risk | インデックスや株の価格の変動不確実性 |
|---|---|
| volatility risk | ボラティリティリスク |
| jump or crash risk | 相場急変動リスク |
| interest rate risk | 金利は直接影響するものじゃないけど、risk-neutral discounting を通して間接的に影響を受ける。 |
| correlation risk | 相関性リスク |
| liquidity risk | 流動性リスク |
| default risk | デフォルトリスク |
上記のリスクの流動性リスクとデフォルトリスク以外のすべてを、これからの議論で扱うことになる。
デフォルトリスクは主要インデックスを扱うような場合にはあまり考えなくて良い。流動性リスクは主要インデックスや商品先物を扱うような場合には問題になることはほとんどない。
Other Risks
モデルを使う事自体のリスクと注文がちゃんと執行されるかという約定リスクもある。
Hedging
いわゆるリスクヘッジについて。ヘッジをうまく使って、投機的ではなく手堅く稼ぐのがOption Writer。
ヘッジの方法には、動的なものと、静的なものの2種類ある。
一般的に、ヘッジプログラムを組む上で唯一の対象や唯一の重要な対象の組み合わせはない。Gilbert et alはヘッジプログラムを実装する上で、可変の(variable ?)年金配給会社、すなわち生命保険の3つの主要な対象を報告した。
| accounting level | 会計能力? |
|---|---|
| accounting volatility | 会計変動性? |
| economic risks | 経済リスク |
この本では accounting issues は意図的に考慮しない。
一般的に言えば、ヘッジプログラムの目的はヘッジした金融商品の対価で完全に複製し、すべてのリスクを抹消することである。だが実際は、2つの主要な問題でこれはほとんど不可能である。1つは、ヘッジの再配分の頻度の問題。2つ目は、市場の不完全性である。
マーケットが完全ならば、ヘッジする人は完全にオプションのキャッシュ・フローリスクを完全に抹消するように務める。マーケットが完全でなければ、リスクを最小限に留めようとする。
Market-Based Valuation as a Process
この本はデリバティブに投資している会社や金融機関の立場をとっている。重要な決定とデリバティブ周辺の適切なビジネスを起業するために、金融機関は以下の根本的な要素を考慮しなければならない。
| market realities | 何がオプションの評価のマーケットを特徴づけているのか |
|---|---|
| market model | 現実的な評価の枠組みを持つもつ理論的なモデルを使うべき |
| vanilla instrument valuation | 大きな評価軸でバニラ商品の価格付ける効率的な手法を持っているべき |
| model calibration | マーケットモデルが最低限満たすべき要素はバニラ商品を合理的に価格付けること |
| exotic instrument valuation | モンテカルロ法のような数学的手法でエグゾティックデリバティブを価値付ける方法がなければならない |
| hedging | デリバティブ商品の価値付けができれば、このヘッジするための情報をそのデリバティブから入手することができる |
多分続きます!


コメント